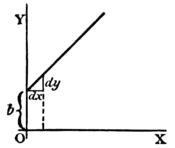
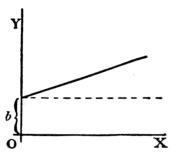
ascends at ${\displaystyle 45^{\circ }}$; for whatever values we give to ${\displaystyle x}$ to the right, we have an equal ${\displaystyle y}$ to ascend. The line has a gradient of ${\displaystyle 1}$ in ${\displaystyle 1}$.

Now differentiate ${\displaystyle y=x+b}$, by the rules we have already learned (pp. 22 and 26 ante), and we get ${\displaystyle {\dfrac {dy}{dx}}=1}$.

The slope of the line is such that for every little step ${\displaystyle dx}$ to the right, we go an equal little step ${\displaystyle dy}$ upward. And this slope is constant–always the same slope.

Fig. 19.	Fig. 20.

(2) Take another case:

We know that this curve, like the preceding one, will start from ${\displaystyle a}$ height ${\displaystyle b}$ on the ${\displaystyle y}$-axis. But before we draw the curve, let us find its slope by differentiating; which gives us ${\displaystyle {\dfrac {dy}{dx}}=a}$. The slope will be constant, at an angle, the tangent of which is here called ${\displaystyle a}$. Let us assign to ${\displaystyle a}$ some numerical value–say ${\displaystyle {\tfrac {1}{3}}}$. Then we must give it such a slope that it ascends ${\displaystyle 1}$ in ${\displaystyle 3}$; or