128
HYDROMECHANICS
[HYDRODYNAMICS
direction θ along a plane boundary, and to give a constant skin velocity over the surface of a jet, where the pressure is constant.
It is convenient to introduce the function
 |
| Fig. 4. |
so that the polygon representing Ω conformally has a boundary given by straight lines parallel to the coordinate axes; and then to determine Ω and w as functions of a variable u (not to be confused with the velocity component of q), such that in the conformal representation the boundary of the Ω and w polygon is made to coincide with the real axis of u.
It will be sufficient to give a few illustrations.
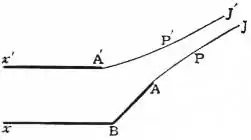
Consider the motion where the liquid is coming from an infinite distance between two parallel walls at a distance xx′ (fig. 4), and issues in a jet between two edges A and A′; the wall xA being bent at a corner B, with the external angle β = 12π/n.
The theory of conformal representation shows that the motion is given by
| ζ = [ | √ (b − a′·u − a) + √(b − a·u − a′) | ] | 1/n | , u = ae−πw/m; |
| √ (a − a′·u − b) |
where u = a, a′ at the edge A, A′; u = b at a corner B; u = 0 across xx′ where φ = ∞; and u = ∞, φ = ∞ across the end JJ′ of the jet, bounded by the curved lines APJ, A′P′J′, over which the skin velocity is Q. The stream lines xBAJ, xA′J′ are given by ψ = 0, m; so that if c denotes the ultimate breadth JJ′ of the jet, where the velocity may be supposed uniform and equal to the skin velocity Q,
If there are more B corners than one, either on xA or x′A′, the expression for ζ is the product of corresponding factors, such as in (5).
Restricting the attention to a single corner B,
| ζn = ( | Q | ) | n | (cos nθ + i sin nθ) = | √ (b − a′·u − a) + √ (b − a·u − a′) | , |
| q | √ (a − a′·u − b) |
| ch nω = ch log ( | Q | ) | n | cos nθ + i sh log ( | Q | ) | n | sin nθ |
| q | q |
| = 12(ζn + ζ−n) = √ | b − a′ | √ | u − a | , |
| a − a′ | u − b |
| sh nΩ = sh log ( | Q | ) cos nθ + i ch log ( | Q | ) | n | sin nθ |
| q | q |
| = 12(ζn + ζ−n) = √ | b − a | √ | u − a′ | , |
| a − a′ | u − b |
and then
| dΩ | = − | 1 | √ (b − a′·b − a′) | , | dw | = − | m | , | |
| du | 2n | (u − b) √ (a − a·u − a′) | du | πu |
the formulas by which the conformal representation is obtained.
For the Ω polygon has a right angle at u = a, a′, and a zero angle at u = b, where θ changes from 0 to 12π/n and Ω increases by 12iπ/n; so that
| dΩ | = | A | , where A = | √ (b − a·b − a′) | . |
| du | (u − b) √ (u − a·u − a′) | 2n |
And the w polygon has a zero angle at u = 0, ∞, where ψ changes from 0 to m and back again, so that w changes by im, and
| dw | = | B | , where B = − | m | . |
| du | u | π |
Along the stream line xBAPJ,
and over the jet surface JPA, where the skin velocity is Q,
| dφ | = −q = −Q, u = aeπsQ/m = aeπs/c, |
| ds |
denoting the arc AP by s, starting at u = a;
| ch nΩ = cos nθ = √ | b − a′ | √ | u − a | , |
| a − a′ | u − b |
| sh nΩ = i sin nθ = i √ | a − b | √ | u − a′ | , |
| a − a′ | u − b |
and this gives the intrinsic equation of the jet, and then the radius of curvature
| ρ = − | ds | = | 1 | dφ | = | i | dw | = | i | dw | / | dΩ | |||
| dθ | Q | dθ | Q | dΩ | Q | du | du |
| = | c | · | u − b | √ (u − a·u − a′) | , | |
| π | u | √ (a − b·b − a′) |
not requiring the integration of (11) and (12)
If θ = α across the end JJ′ of the jet, where u = ∞, q = Q,
| ch nΩ = cos nα = √ | b − a′ | , sh nΩ = i sin nα= i √ | a − b | , |
| a − a′ | a − a′ |
Then
| cos 2nα − cos 2nθ = 2 | a − b·b − a′ | = 12sin2 2nα | a − a′ |
| a − a′·u − b | u − b |
| sin 2nθ = 2 | √ (a − b.b − a′) √ (u − a·u − b′) |
| a − a′·u − b |
| = sin 2nα | √ (a − a·b − a′) | ; |
| u − b |
| 2n | c | ( 1 + | b | ) | √ (a − b·b − a′) | |
| φ | ρ | u − b | √ (u − a·u − a′) |
| = | a − a′ + (a + a′) cos 2nα − [ a + a′ + (a − a′) cos 2nα ] cos 2nθ | × | cos 2nα − cos 2nθ | . |
| (a − a′) sin2 2nα | sin 2nθ |
Along the wall AB, cos nθ = 0, sin nθ = 1,
| ch nΩ = i sh log ( | Q | ) | n | = i √ | b − a′ | √ | a − u | , |
| q | a − a′ | u − b |
| sh nΩ = i ch log ( | Q | ) | n | = i √ | a − b | √ | u − a′ | , |
| q | a − a′ | u − b |
| ds | = | ds | dφ | = | m | = | c | Q | ||
| du | dφ | dt | πqu | π | qu |
| π | AB | = ∫ab | Q | du | ∫ [ | √ (a − b) √ (u − a′) + √ (b − a′) √ (a − u) | ] | 1/n | du | . | ||
| c | q | u | √ (a − a′) √ (u − b′) | u |
Along the wall Bx, cos nθ = 1, sin nθ = 0,
| ch nΩ = ch log ( | Q | ) | n | = √ | b − a′ | √ | a − u | , |
| q | a − a′ | b − u |
| sh nΩ = sh log ( | Q | ) | n | = √ | a − b | √ | u − a′ | . |
| q | a − a′ | b − u |
At x where φ = ∞, u = 0, and q = q0,
| ( | Q | ) | n | = √ | b − a′ | √ | a | + √ | a − b | √ | −a′ | . |
| q0 | a − a′ | b | a − a′ | q |
In crossing to the line of flow x′A′P′J′, ψ changes from 0 to m, so that with q = Q across JJ′, while across xx′ the velocity is q0, so that
| JJ′ | = | q0 | [ √ | b − a′ | √ | a | − √ | a − b | √ | −a′ | ] | 1/n | , |
| xx′ | Q | a − a′ | b | a − a′ | b |
giving the contraction of the jet compared with the initial breadth of the stream.
Along the line of flow x′A′P′J′, ψ = m, u = a′e−πφ/m, and from x′ to A′, cos nθ = 1, sin nθ = 0,
| ch nΩ = ch log ( | Q | ) | n | = √ | b − a′ | √ | a − u | , |
| q | a − a′ | b − u |
| sh nΩ = sh log ( | Q | ) | n | = √ | a − b | √ | u − a′ | . |
| q | a − a′ | b − u |
Along the jet surface A′J′, q = Q,
| ch nΩ = cos nθ = √ | b − a′ | √ | a − u | , |
| a − a′ | b − u |
| sh nΩ = i sin nθ = i √ | a − b | √ | u − a′ | . |
| a − a′ | b − u |
giving the intrinsic equation.
41. The first problem of this kind, worked out by H. v. Helmholtz, of the efflux of a jet between two edges A and A1 in an infinite wall, is obtained by the symmetrical duplication of the above, with n = 1, b = 0, a′ = −∞, as in fig. 5,
| ch Ω = √ | u − a | , sh Ω = √ | − a | ; |
| u | u |
and along the jet APJ, ∞ > u = aeπs/c > a,
| sh Ω = i sin θ − i √ | a | = ie−1/2 πs/c, |
| u |
| PM = ∫∞s sinθ ds = ∫ e−12πs/c ds = | c | e−1/2 πs/c = | c | sin θ, |
| 12π | 12π |