AND CANALS]
HYDRAULICS
69
to the direction of motion is treated as sliding down the channel to a′a′b′b′ without deformation. The component of the weight parallel to the channel bed balances the friction against the channel, and in estimating the friction the velocity of rubbing is taken to be the mean velocity of the stream. In actual streams, however, the velocity of rubbing on which the friction depends is not the mean velocity of the stream, and is not in any simple relation with it, for channels of different forms. The theory is therefore obviously based on an imperfect hypothesis. However, by taking variable values for the coefficient of friction, the errors of the ordinary formulae are to a great extent neutralized, and they may be used without leading to practical errors. Formulae have been obtained based on less restricted hypotheses, but at present they are not practically so reliable, and are more complicated than the formulae obtained in the manner described above.
§ 96. Steady Flow of Water with Uniform Velocity in Channels of Constant Section.—Let aa′, bb′ (fig. 103) be two cross sections normal to the direction of motion at a distance dl. Since the mass aa′bb′ moves uniformly, the external forces acting on it are in equilibrium. Let Ω be the area of the cross sections, χ the wetted perimeter, pq + qr + rs, of a section. Then the quantity m = Ω/χ is termed the hydraulic mean depth of the section. Let v be the mean velocity of the stream, which is taken as the common velocity of all the particles, i, the slope or fall of the stream in feet, per foot, being the ratio bc/ab.
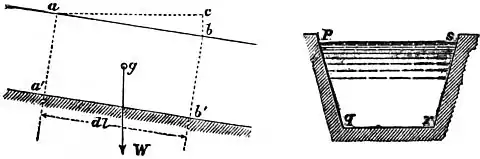
Fig. 103.
The external forces acting on aa′bb′ parallel to the direction of motion are three:—(a) The pressures on aa′ and bb′, which are equal and opposite since the sections are equal and similar, and the mean pressures on each are the same. (b) The component of the weight W of the mass in the direction of motion, acting at its centre of gravity g. The weight of the mass aa′bb′ is GΩ dl, and the component of the weight in the direction of motion is GΩdl × the cosine of the angle between Wg and ab, that is, GΩdl cos abc = GΩ dl bc/ab = GΩidl. (c) There is the friction of the stream on the sides and bottom of the channel. This is proportional to the area χdl of rubbing surface and to a function of the velocity which may be written ƒ(v); ƒ(v) being the friction per sq. ft. at a velocity v. Hence the friction is −χ dl ƒ(v). Equating the sum of the forces to zero,
| GΩi dl − χ dl ƒ(v) = 0, ƒ(v) / G = Ωi / χ = mi. |
(1) |
But it has been already shown (§ 66) that ƒ(v) = ζGv2/2g,
| ∴ ζv2 / 2g = mi. | (2) |
This may be put in the form
| v = √ (2g/ζ) √ (mi) = c √ (mi); | (2a) |
where c is a coefficient depending on the roughness and form of the channel.
The coefficient of friction ζ varies greatly with the degree of roughness of the channel sides, and somewhat also with the velocity. It must also be made to depend on the absolute dimensions of the section, to eliminate the error of neglecting the variations of velocity in the cross section. A common mean value assumed for ζ is 0.00757. The range of values will be discussed presently.
It is often convenient to estimate the fall of the stream in feet per mile, instead of in feet per foot. If ƒ is the fall in feet per mile,
Putting this and the above value of ζ in (2a), we get the very simple and long-known approximate formula for the mean velocity of a stream—
| v = 14 12 √ (2mf). | (3) |
The flow down the stream per second, or discharge of the stream, is
| Q = Ωv = Ωc √ (mi). | (4) |
§ 97. Coefficient of Friction for Open Channels.—Various expressions have been proposed for the coefficient of friction for channels as for pipes. Weisbach, giving attention chiefly to the variation of the coefficient of friction with the velocity, proposed an expression of the form
| ζ = α (1 + β/v), | (5) |
and from 255 experiments obtained for the constants the values
This gives the following values at different velocities:—
| v = ζ = | 0.3 0.01215 | 0.5 0.01025 | 0.7 0.00944 | 1 0.00883 | 112 0.00836 | 2 0.00812 | 3 0.90788 | 5 0.00769 | 7 0.00761 | 10 0.00755 | 15 0.00750 |
In using this value of ζ when v is not known, it is best to proceed by approximation.
§ 98. Darcy and Bazin’s Expression for the Coefficient of Friction.—Darcy and Bazin’s researches have shown that ζ varies very greatly for different degrees of roughness of the channel bed, and that it also varies with the dimensions of the channel. They give for ζ an empirical expression (similar to that for pipes) of the form
| ζ = α (1 + β/m); | (6) |
where m is the hydraulic mean depth. For different kinds of channels they give the following values of the coefficient of friction:—
| Kind of Channel. | α | β | |
| I. | Very smooth channels, sides of smooth cement or planed timber | .00294 | 0.10 |
| II. | Smooth channels, sides of ashlar, brickwork, planks | .00373 | 0.23 |
| III. | Rough channels, sides of rubble masonry or pitched with stone | .00471 | 0.82 |
| IV. | Very rough canals in earth | .00549 | 4.10 |
| V. | Torrential streams encumbered with detritus | .00785 | 5.74 |
The last values (Class V.) are not Darcy and Bazin’s, but are taken from experiments by Ganguillet and Kutter on Swiss streams.
The following table very much facilitates the calculation of the mean velocity and discharge of channels, when Darcy and Bazin’s value of the coefficient of friction is used. Taking the general formula for the mean velocity already given in equation (2a) above,
where c = √ (2g/ζ), the following table gives values of c for channels of different degrees of roughness, and for such values of the hydraulic mean depths as are likely to occur in practical calculations:—
Values of c in v = c √ (mi), deduced from Darcy and Bazin’s Values.
| Hydraulic Mean. Depth = m. | Very Smooth Channels. Cement. | Smooth Channels. Ashlar or Brickwork. | Rough Channels. Rubble Masonry. | Very Rough Channels. Canals in Earth. | Excessively Rough Channels encumbered with Detritus. |
| .25 | 125 | 95 | 57 | 26 | 18.5 |
| .5 | 135 | 110 | 72 | 36 | 25.6 |
| .75 | 139 | 116 | 81 | 42 | 30.8 |
| 1.0 | 141 | 119 | 87 | 48 | 34.9 |
| 1.5 | 143 | 122 | 94 | 56 | 41.2 |
| 2.0 | 144 | 124 | 98 | 62 | 46.0 |
| 2.5 | 145 | 126 | 101 | 67 | .. |
| 3.0 | 145 | 126 | 104 | 70 | 53 |
| 3.5 | 146 | 127 | 105 | 73 | .. |
| 4.0 | 146 | 128 | 106 | 76 | 58 |
| 4.5 | 146 | 128 | 107 | 78 | .. |
| 5.0 | 146 | 128 | 108 | 80 | 62 |
| 5.5 | 146 | 129 | 109 | 82 | .. |
| 6.0 | 147 | 129 | 110 | 84 | 65 |
| 6.5 | 147 | 129 | 110 | 85 | .. |
| 7.0 | 147 | 129 | 110 | 86 | 67 |
| 7.5 | 147 | 129 | 111 | 87 | .. |
| 8.0 | 147 | 130 | 111 | 88 | 69 |
| 8.5 | 147 | 130 | 112 | 89 | .. |
| 9.0 | 147 | 130 | 112 | 90 | 71 |
| 9.5 | 147 | 130 | 112 | 90 | .. |
| 10.0 | 147 | 130 | 112 | 91 | 72 |
| 11 | 147 | 130 | 113 | 92 | .. |
| 12 | 147 | 130 | 113 | 93 | 74 |
| 13 | 147 | 130 | 113 | 94 | .. |
| 14 | 147 | 130 | 113 | 95 | .. |
| 15 | 147 | 130 | 114 | 96 | 77 |
| 16 | 147 | 130 | 114 | 97 | .. |
| 17 | 147 | 130 | 114 | 97 | .. |
| 18 | 147 | 130 | 114 | 98 | .. |
| 20 | 147 | 131 | 114 | 98 | 80 |
| 25 | 148 | 131 | 115 | 100 | .. |
| 30 | 148 | 131 | 115 | 102 | 83 |
| 40 | 148 | 131 | 116 | 103 | 85 |
| 50 | 148 | 131 | 116 | 104 | 86 |
| ∞ | 148 | 131 | 117 | 108 | 91 |
§ 99. Ganguillet and Kutter’s Modified Darcy Formula.—Starting
from the general expression v = c√mi, Ganguillet and Kutter
examined the variations of c for a wider variety of cases than those
discussed by Darcy and Bazin. Darcy and Bazin’s experiments
were confined to channels of moderate section, and to a limited
variation of slope. Ganguillet and Kutter brought into the discussion
two very distinct and important additional series of results.
The gaugings of the Mississippi by A. A. Humphreys and H. L.
Abbot afford data of discharge for the case of a stream of exceptionally
large section and or very low slope. On the other hand, their
own measurements of the flow in the regulated channels of some