Can a radioactive moon affect life on a planet?

Question

This question is meant as a reality check on this answer to The land grows evil and corrupted ... but why?

Radioactive moon in a nearly geosynchronous orbit. It slowly kills or alters all life exposed to it, but it doesn't hang perfectly still in the night sky.

It travels very slowly, circling the planet once every 500+ years, enough time for the far side of the planet to recover from its ill effects. People are forced into migrating every 500+ years to avoid the bad moon.

OK, I want to reality-check that. Could that work?

What I'm not interested in:

1. Ignore how was it even formed.
2. Ignore how humans evolved.
3. About two thousands years ago it just came to be, OK? Orbit is stable, it didn't wreak havoc on another moons orbits (or if it did, it is out of scope, it's OK now).

What I want to reality-check:

1. Could it be radioactive enough to cause significant cancer increase, radiation sickness and mutations?
2. Could that happen without moon exploding?
3. Could it work for 2000 years (that is merely 4 migrations)? I'm OK with "now it is not nearly as scary as in legends" here.
4. Could it affect patch significantly smaller than a whole hemisphere?

All of the above partial questions boil down to: What would be composition of this moon, or why it is impossible?

Answer 1

How to generate radiation

Radiation by nuclear emission

A moon made of some non-fissile (definitely not fissile!) transuranic element would emit significant alpha, beta, and/or gamma radiation.

Radiation by neutron generation

The moon would have to be a neutron generator. There are a few ways to create neutrons, but they involve things like fission reactors and hydrogen ion linear accelerators. This would basically have to be an alien space station, not a moon. I think that is outside the scope of the question, so I'll ignore neutron radiation.

Radiation by magnetic field

A moon filled with a magneto-hydro-dynamically active fluid would be able to generate a significant magnetic field, the way that Jupiter does. This field will trap charged particles. If something emits lots of charged particles (Io does this for Jupiter; the solar wind may be sufficient for Earth since it is closer to the Sun) then those particles can be trapped to form a high energy plasma in the magnetic field. This is analogous to the Van Allen belts around Earth, though they would be stronger with a stronger magnetic field.

Once you have a very strong magnetic field and very high energy particles in that field (in the keV, 10 million K range), you can emit energy by slamming these particles into something else, namely the atmosphere. This is an aurora. Much of Jupiter's emissions come from its aurorae, while some come from Io and its thin ionosphere passing through Jupiter's magnetically maintained high energy plasma disk.

Jupiter's magnetic field emits radio waves at ~100 GW in the 10-100 m wavelength; IR at ~50 TW in the 3-14 $\mu m$ range; and UV at ~10 TW in the 80-180 nm range. By comparison, Earth's magnetosphere emits only in the radio range at about 0.1 GW.

Radiation by accretion

To generate other wavelengths, like a powerful X-ray source, you need to drop matter into a high gravity object, like a neutron star or a black hole. I don't see any other way for a moon to be an X-ray source, and since this doesn't seem to meet the OP's requirements, I'm going to ignore X-ray radiation.

How radioactive will these sources be?

Alpha and beta radiation

Alpha and beta particles have little to no ability to penetrate the atmosphere, so they are basically out as radiation sources.

Gamma (and X-ray) radiation

Gammas are another story. If the moon were made of something that had a long half-life but emitted gamma radiation, then maybe it would be a potent source.

There are a great variety of metal isotopes with long half-lives (1e5 years +) that emit x-ray radiation in the 5-10 keV range; decay of non-fissile transuranics provides a wide spectrum of emissions in the x-ray to gamma range (up to 15 MeV). This could be nice and deadly, but unfortunately, the atmosphere is a very good absorber of X-rays and gamma radiation.

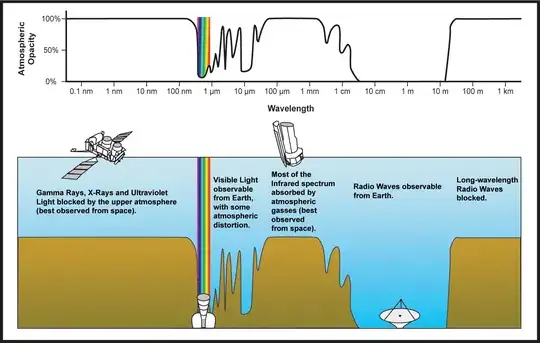
The attenuation coefficients in air of various energy radiation can be found here. For a 10 keV X-ray, the density coefficient of attenuation ($\mu/\rho$) is 5.12 cm$^2$/g. Multiply this by the density of air (1.2 mg/cm$^3$) and convert to meters for a coefficient ($\mu$) of 6.3 meters$^{-1}$. A half-thickness can be obtained from an attenuation coefficient by dividing the log of 2 by the attenuation constant; the half-thickness for 10 keV X-ray penetration is 0.11 meters. That means, each 0.11 meters drops the power of X-ray radiation in half. Needless to say, X-rays won't make it far in the air.

Gamma rays do better, but not by much. For 1 MeV gamma rays, the half thickness is up to about 9 meters. For 10 MeV gammas it is 28 meters. 28 meters is a serious distance to penetrate, but not so much compared to the thickness of the Earth's atmosphere. For a simulated constant density atmosphere at the density we are using to calculate, the Earth's atmosphere would be about 8 km thick. Divide that distance by 28 and you get 289; so gamma energy from space is reduced by a factor of $2^{289}$ by the time it reaches the surface, not enough to do any damage. A radioactive object in orbit just won't do the trick.

Magnetically induced radiation - Decametric radio

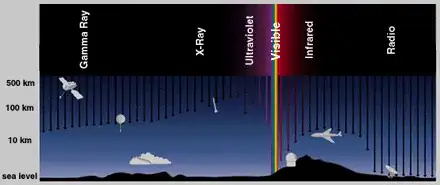
Here is where we get more interesting. Jupiter's aurorae, i.e. the regions where the magnetic field lines intersect with the atmosphere, are extremely powerful radio emitters. You may notice from the above graphic, or from listening to the radio in your car, that radio waves penetrate the atmosphere nicely. The 10cm to 10m band of little atmospheric attenuation corresponds to the 3-300 MHz range; VHF and UHF radio. Here is Jupiter's (and other planets') radio emissions.

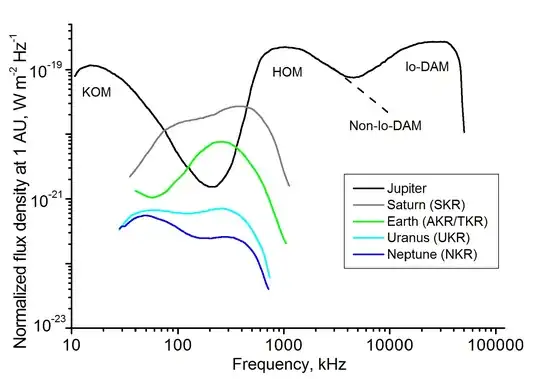
The decametric radiation (DAM) in this graph is largely controlled by interactions with the moon Io. The mechanics of these interactions are mostly beyond me, so I can only suggest that there are possible mechanisms for getting large scale radio wave energy released. First, there can be an orbiting satellite which is a massive magnetic field generator for some reason. This satellite acts like Jupiter, while the Earth acts like Io. The magnetic field lines of this satellite interact with the Earth's so that high-energy charged particles captured in the combined magnetic fields are funneled into Earth's poles. This forms powerful aurorae, with tremendous radio emissions.

The last bit of assuming we have to make is that this interaction will be able to create the appropriate decametric radio emissions without putting out too much energy in other frequencies. I am not sure if that is possible at the high energies that his system will require, but I am willing to assume it. We want radio emission to penetrate the Earth's atmosphere cleanly, heating the surface without heating the atmosphere more than it needs to.

Radio wave attenuation in the atmosphere is in the 3-10 db range. Taking an optimistic view, that means that 10-50% of the radio energy will reach the ground, while 50-90% remains in the atmosphere. Once VHF energy hits the ground, nearly all of it will be absorbed.

The goal here will be to get the ground to absorb a lot of radiation, making the ground too hot to support life. The aurora are localized effects; if they occur at an altitude of 100 km, then only a circle about 1000 km in radius is affected. If the aurora were directly over the North pole, for example, the arctic circle would not receive any radiation; it would be blocked by the curvature of the earth.

For the region directly below the aurora, we would like to up the incident radiation by a substantial amount to make the place lifeless. The incident radiation that is absorbed the the surface on Earth averages to 163 W/m$^2$ over the whole surface over a whole year. Let's say our target is to hit the surface with an additional 250 W/m$^2$ in radio energy at the sub-aurora point to sterilize it.

For a low attenuation scenario of 50% atmospheric absorption, an aurora occurring at 100 km must deliver an equivalent to 500 W/m$^2$ at that altitude. At 100 km, the surface area of this radiation would be $4.2\times10^{10}$ m$^2$; so the radio luminosity of a point source must be just about 2 TW. This compares with 0.1 GW distributed over the Earth's entire magnetosphere, or ~40 GW from Jupiter's radio emissions. So this is a lot, but perhaps in the realm of possibility.

In order for the 'moon' object to work, it would have to be in orbit of Earth, but not necessarily geosynchronous orbit. Any object of moon-like size 'could' generate the desired magnetic fields, but it would surely be artificial. It would have to be filled with some sort of magnetic fluid that generated the magnetic fields. Again, this is not my specialty, but I suspect that a very high temperature, low viscosity, high flow rate iron core would work; as would a liquid hydrogen core, as on Earth.

However, having this in a moon-sized object would surely be artificial.

Conclusion

In this scenario, there is an orbiting object that generates extremely high magnetic fields. It is probably artificial. These fields cause solar wind particles to be trapped around the object. When these lines link up with the Earth's in a certain way, the charged particles are discharged into the Earth's atmosphere; there they collide with atmospheric molecules and release radio waves.

Much of the radio waves end up back in space, but the sub-aurora point is hit with the equivalent of equatorial daylight sun, constantly. If these magnetic effects are stable, then within a few days, the ground within a hundred km has heated considerably, and within a week, plant life is being killed by the heat. If the aurora stays in place for at least a month, there will be a dead patch a hundred km across, where nothing survives except bacteria. The auroras are stable for a while, until the magnetic lines drift off, then soon another aurora will pop nearby. Some aurora are so far north that they just melt glaciers to bare rock and are done, others are over the ocean. But when they appear at mid-latitudes over land, beware!

This doesn't meet the geosynchonous criteria, but it would explain why dead spots would appear on a time scale of months in northern latitudes.

Answer 2

I'm going to take this a slightly different direction and say that yes, radiation from a moon can indeed affect life on a planet, just not quite in the same way intended by the answer you linked.

As others have explained, our atmosphere and magnetosphere do a good job of protecting the planet from most external radiation. The main type of radiation they allow through is visible light. If you wanted a moon to radiate something that wreaked havoc on the portion of the planet it faced, have the moon reflect (or absorb and re-emit) light in a specific, narrow portion of the color spectrum. Plants and other photosynthesizing organisms use different portions of the light spectrum differently. A significant increase in one color band could unbalance an entire ecosystem, perhaps by causing certain bacteria or other microscopic life form to thrive and grow too rapidly. This sudden overabundance can deplete the oxygen in water or release toxic substances. Either of these can easily lead to die-offs of marine life, and the effects trickle up the food chain from there. Toxic water makes it harder for plants to grow (especially if the toxin can evaporate and then be pulled down by rainfall), and fewer plants means that animals are more likely to over-graze.

People that live nearby would observe that once the moon becomes visible, fish start dying off, water supplies become poisonous to humans, plants stop thriving, and most land/air animals migrate away. Other animals migrate in, creatures who are better adapted to the new conditions. The entire ecosystem gets thrown out of balance, taking many years to completely recover. Your 500 year cycles means that there's plenty of time to recover, though, so balance eventually returns.

So yes, it's entirely possible that a moon could radiate energy that has a significant impact on the planet, just not necessarily in the traditional "nuke it with gamma rays" sense.

Answer 3

Could it be radioactive enough to cause significant cancer increase, radiation sickness and mutations?

Not here, probably not elsewhere either

A radioactive moon could give out radiation in five forms:

• Alpha particles: essentially an electronless helium-4 nucleus. Doesn't travel farther than a few centimeters/inches in an atmosphere, so no danger at all.

• Beta particles: an electron or positron travelling at high speeds. Travels further in air, but still doesn't go farther than a few meters/yards.

• Free neutrons: this is the only radiation form that can make something else radiactive too. Can go a few kilometers/miles in an atmosphere, but we got a lot of atmosphere anyway.

• X-rays: needs no explanation.

• Gamma rays: ditto.

Only the two latter ones are scary. But we have a shield in the form of an ozone layer, which already handles those quite well.

So the only place where a radioactive moon would be dangerous would be on a planet without an ozone layer or similar shielding, but in that case you are pretty much [expletive] anyway.

That being said, you could make the whole moon out of uranium if you wish. We'd still be safe.

Could that happen without moon exploding?

Sure. In order for it to explode it would have to be so hot that it would become gaseous. It would need to be as hot as a star. But it would have to be way more massive than Jupiter for that to happen.

Could it work for 2000 years (that is merely 4 migrations)?

It could reallistically stay there as long as our own Moon can.

Could it affect patch significantly smaller than a whole hemisphere?

Nope.

Answer 4

If the moon circled the planet every 500 years and was in geosynchronous orbit, the planet would have a day 500 years long! Oh, you said nearly geosynchronous orbit. What you seem to mean is the moon actually orbits the planet many times in 500 years, but the position of the spot directly beneath the moon slowly circles around the planet every 500 years.

Earth like life needs relatively short day/night cycles, so if the planet is like Earth and the people and their plants and animals are like humans and earth life, they will probably need relatively short day/night cycles to keep the planet from heating up too much during the day and cooling too much during the night.

So if the planet is exactly like Earth exactly synchronous orbit would take exactly one day and there would be about 365.25 days in a year and so in 500 years there would be about 182,625 days. 360 arc degrees in a circle divided by 182,625 is 0.0019712 degrees. 21,600 arc minutes divided by 182,625 is 0.1182751. 1,296,000 arc seconds divided by 182,625 is 7.09650 arc seconds.

Thus the moon would not appear exactly stationary in the sky but would move by 7.09650 arc seconds, or 0.1182 arc minutes, or 0.0019712 arc degrees every day. It would take the apparent position of the moon 845.52295 days to move by one arc degree, about twice the apparent width of the moon. since one degree on Earth is about 60 miles, it would take about 2.3149 years for the sub moon spot to move by about 60 miles.

Note: Assuming a natural satellite or moon orbiting a planet that is exactly like Earth, geosynchronous orbit would be well outside the Roche limit that would cause a moon to break up, so the moon in geosynchronous orbit should be fine.

So it would be possible for a moon to be positioned nearly in geosynchronous orbit of an Earth duplicate with enough of a difference for the spot on the planet directly below the moon to circle the planet every 500 years.

But the idea that a radioactive moon could kill life exposed to it's radiation seems implausible because the Earth's atmosphere, magnetic field, and ozone layer block most forms of dangerous radiation from Earth's surface. If you change them enough that a radioactive moon can kill life on the planet, you change them enough that solar radiation, solar wind, and cosmic rays will probably kill all life on the planet everywhere anyway, so getting out from under the radioactive moon won't do the life any good.

So you need some other way for a moon to kill at least some life on the planet.

If the moon orbits the planet in exactly the same plane that the planet orbits the sun, the moon is likely to be eclipsed around midnight by the shadow of the planet. But if the moon's orbit is titled a little it will never be eclipsed but remain in sunlight all through the planetary midnight.

And maybe near the center of the planet facing side of the moon there is a large crater with an almost parabolic cross section and a smooth, mirror like reflective surface. And the parabolic shape happens to have a focal point near the surface of the planet. That would be quite a coincidence, or maybe the work of malevolent super advanced aliens.

So around midnight, as the far side of the planet has cooled a lot from the daytime heating, the sub moon location get a big blast of light and heat reflected from the moon. So the sub moon location will not cool down as much during the night as the rest of the planet's surface, and so will get hotter and hotter day after day after day. And this superheated region of the planet will move around very slowly.

Hot land or water heats up the air above it. Hot air rises, and forms low pressure zones from the surface it rises from. And low pressure zones caue wind circulation which forms storms. Thus the planet could have a permanent hurricane with the eye at the sub moon spot and perhaps having damaging winds spread over most of the hemisphere. And the eye of that hurricane would slowly move a few miles per year.

That would not kill all life on the hemisphere but would force Humans who grew crops that would be destroyed by the winds to slowly migrate ahead of the hurricane.

Answer 5

Our planet has a strong magnetosphere that protects us from external radiation. This could be unusual - Venus doesn't have one, Mars a residual but extremely weak one. This is why some people are a little worried about Mars colonisation - Curiosity measured the radiation from the sun at 300 mSv over 180 days. That's about 6x the maximum dose for a nuclear worker. So lets say your planet doesn't have one.

You could have a planet mainly made of uranium (like the way Mercury is mainly iron) - this could give you something like the Oklo Natural Nuclear Reactor If the more radioactive isotopes condensed into a core or around the core that could maybe give you something a bit like a breeder reactor or a travelling wave reactor.

An unshielded reactor (530Sv), in orbit at 17000km(Mars synchronous), gives me an exposure of 1.6Sv per year using this - but only if its 1,000,000x bigger than Fukushima. For the earth - it would need to be 42000km(Geosynchronous), gives me an equivalent exposure at around 5,000,000x bigger than Fukushima.

You could reduce the mass needed by increasing the rotation of the planet - if the earth rotated every 90 minutes, then geosynchronous would be 160 miles(209km) high. That would give you one reactor, giving 1Sv exposure to the surface.

Answer 6

TL/DR: Its not the ionising radiation, but the heat output that kills you

As mentioned in other answers, the ionising radiation from a radioactive moon would be blocked by the atmosphere and not really do a lot. But a radioactive moon also generates heat, and depending how radioactive it is, that could be enough to destroy life on earth.

Solar irradiance is 1361 W/m2 at the top of the atmosphere. If that increases by 10%, the average temperature of the planet will increase to 46°C, which will start a runaway greenhouse effect that will evaporate the oceans. The runaway greenhouse effect comes from water vapor, which is a greenhouse gas, and at an average temperature of 46°C there will be enough water vapor in the atmosphere to start the runaway greenhouse.

If the moon were made of uranium-238, it would probably explode in a giant nuclear explosion, but let's assume it does not. (Edit: Uranium-238 does not sustain a chain reaction so it won't explode) Uranium-238 is actually one of the least-radioactive radioactive elements we know. It only generates $0.1$ watt per ton of decay heat. The moon has a mass of $7.34\cdot 10^{19}$ tonnes. If it would be made of uranium-238 it would generate $7.34\cdot 10^{18}$ watt of decay heat. The moon is $384400$ km from the earth. So the irradiance of the moon made of uranium-238 on earth would be $$\dfrac{7.34\cdot 10^{18}}{\pi \cdot(384400\cdot 1000)^2} = 15.8 \space\text{watt/m}^2$$

So that is not that significant, but it is only a factor of 9 away from the $136 \space W/m^2$ needed to evaporate the oceans. So if you choose basically any other radioactive material to construct your moon from, or make the moon a bit more massive, or put it closer to earth (irradiance scales with distance squared), the heat output will easily be enough to boil the oceans. At $136\space w/m^2$ that will be a slow process probably taking thousands of years, but there are many much more radioactive materials to be found. You can easily increase the heat output of the radioactive decay moon by a million or more, which would instantly fry life on earth.

The moon is a disk of the same diameter as the sun as seen from earth, so the thermal radiation will also have the same wavelength as the sun when the intensity is the same. At $136\space w/m^2$ the moon would be somewhere around red or yellow-hot, but if you increase the heat output a lot the moon will appear white- or blue hot depending on which temperature you choose. Though if the absolute heat output from the moon is too big, the radiation pressure itself will probably overcome the moon's gravity and start to evaporate the moon. But a more massive moon also increases its gravity, so just something to balance.

One other option: UV radiation

The above thermal radiating moon gave me another idea: if the moon emits strong ultraviolet light that will do more or less what you want. Make the moon denser, so you have less surface area, so temperatures will be higher for a given radiation output. If the moon's surface temperature is around 8000 Kelvin the peak radiation is in the UV-A, and there is significant UV-B too. UV-A is not absorbed by the ozone layer, and UV-B only partially. Normal solar radiation only has 10% of its energy in ultraviolet, so the irradiance of this moon will only need to be a fraction of the solar irradiance to cause a lot of damage. There is still the problem that if you double the natural ultraviolet irradiance in this way, that also increases the heat received by earth by 10%, triggering the runaway greenhouse effect described above. And doubling the ultraviolet will increase the incidence of skin cancer, but not immediately make one side of the planet uninhabitable. But if you decrease the solar output a little bit, or place earth a little bit further away from the sun, this might work. The changes in heat received will change the climates, and the moon's heat only reaching one side of earth will do that even more, but I suppose that's also out of scope.

Answer 7

How about something more indirect?

Say the world is the site of a partially successful colonization project. The "moon" is the last remaining power satellite from the constellation that powered the terraforming process, having drifted out of its geostationary orbit after losing stationkeeping but otherwise still active. When it's overhead, forgotten terraforming/weather control machinery on the surface activates and runs unattended, with adverse effects on the surroundings.

The descendants of the colonists might have adapted to the current state of the planet or become reliant on parts of its native life, and see the terraforming as harmful, or it might just cause harm due to malfunction and lack of control.

Certain areas might be relatively sheltered due to geography and weather patterns, or due to local failures of the terraforming machines.