A nuclear powered, supercritical steam rocket is probably your best bet.
However, you're dealing with some serious engineering problems here, not the least of which is reaction mass.
These kinds of travel paths are known as brachistochrone paths (for shortest time-distance), and require a lot of acceleration.
The good thing though is this acceleration helps you as you can use it to generate your artificial gravity.
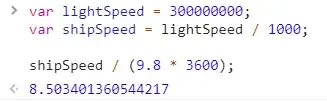
For example, if we want to fly to Mars at Earth gravity, that's 1G acceleration, and per the equations of motion, this would allow you to reach Mars in about 1.3 days when the two planets are at their closest (roughly 55 million km).
This all sounds great, but it's highly unlikely you'd be able to maintain 1G of acceleration for the entire ride. The reason being that to maintain 1G of acceleration on your spacecraft for the entire hour-long trip, you would need a massive amount of fuel. This comes from the thrust-to-weight ratio of your rocket, as well as its specific impulse. The specific impulse is essentially the amount of time you can fire your engines for 1 kg of propellant. So if you determine you need to fire your thrusters for 100,000 seconds (roughly a day), and you can carry 1 million kg of propellant, you'd need an Isp of 1x106/100000 = 10. 10 is an extremely low Isp,
You'd have to calculate whether 1 million kg of propellant (1000 metric tons) can actually accelerate your ship at 1G. The problem is, to move your ship, you also have to move that 1 million kg of propellant. This is the tyranny of the rocket equation.
Another problem is that high efficiency rocket engines (i.e. high Isp) also tend to have low thrust-to-weight ratios, and so low acceleration. This isn't always true, and in a nuclear supercritical steam rocket, it's least likely to be true, but it's still a difficult trade-off.
But there is a silver lining here: the time it takes to travel a certain distance at a certain acceleration is the square root of that distance divided by the acceleration, so if you half the acceleration, you don't necessarily double the travel time.
For example, if we instead accelerate at Moon gravity (1/6th that of Earth), the travel time only jumps to 3 days. This also pushes the Isp we need down, and thus can lower our fuel needs.
If we run through our equation again, 1x106/260000 = 4, so our Isp requirements have dropped significantly. If your Isp is higher, you can get away with carrying less fuel, so let's fix our supercritical steam rocket's Isp at 800. This is very high efficiency, but it's not outside of the theoretical rating for a nuclear supercritical rocket.
Roughly 88% of a rocket's mass is used up getting it to low Earth orbit, however, if we assume our spaceship is already in LEO, our mass requirements drop. So let's say we can get away with 60%. Let's see how our rocket does now.
Per the rocket equation, to get from Earth to Mars in 3 days requires a change in velocity of 55x109 / 2.6x105 = 211 km/s.
Plugging this into the rocket equation for our mass fraction of 60%, we get a delta V of 3.3 km/s (!!). this is a factor of 100 too small, so what do we do?
If our delta-v and our Isp are fixed, the only thing we can play with is the mass fraction. So what mass fraction allows us to accelerate at 1/6 G for 3 days?
Per the rocket equation, assuming our empty spacecraft weighs about 100 metric tons (roughly the mass of the ISS), we need roughly 10 TRILLION metric tons of propellant. So we're screwed. We have to increase our Isp, thus making our rocket more efficient, or we have to lighten the rocket, or we have to relax our flight time. At this point, we basically have to give up on using the acceleration to create our artificial gravity.
So what can we do? Well, we can already put a space probe on Mars in about 3 months flight time, so let's assume we have more technology than a basic boring chemical rocket and go from there. What if we want to get to Mars in a month?
Well this gives us a required average acceleration of 1.5x10-6 m/s2 and a delta-V of 418 m/s. Really though, the only thing that matters here is the delta-V, because we can essentially use any acceleration that gets us to the desired delta-V, then coast along for the rest of the ride (the only reason we wanted to maintain a specific acceleration before was for artificial gravity).
Plugging through the rocket equation, this gives us a much more manageable reaction mass requirement of 5480 kg of propellant, or about 5 metric tons.
So what's going on here? Why the huge disparity? Well, the rocket equation has a natural log in it which turns into an exponent when we try to solve backwards.
This means that the shorter you want your travel time to be, the higher your acceleration needs to be, which in turn makes your reaction mass requirements rise exponentially.
Note that this is a gross oversimplification of the math involved. If you actually want to use brachistochrone paths, your velocity isn't constant for the whole flight, which affects your travel time and delta-V calculations.
However, by using the linked equations you can play around with the math and get good rules of thumb for how long travel should take in your universe. Want things to go faster or slower? Play with the Isp without losing thrust-to-mass ratio. Want to see if you can get a reasonable travel time for a given Isp? Then fix the impulse and delta-V to see if you can get a reasonable reaction mass requirement.