Can a human crew handle cyclic extended high relativistic speed operations?

Question

This question hopes to make a space tug crew's life tolerable.

A supply pipeline links two civilizations. Due to the long travel time between the ends, cargo is "thrown" at the other side in unmanned and unpowered cargo barges, save for minor attitude, yaw and pitch thrusters. Tugs using antimatter drives developed with alien engineering plans push a barge up to 0.1c and release it, then reverse to catch an inbound barge coming at them at 0.1c. Barges are timed like this to prevent a tug going out or coming back with no payload.

(Space tug)

The human crew is going to be subjected to an environment for a long time, and will be doing this repeatedly. My goal is to:

• Minimize the duration of each operation

• Minimize exposure to either low or high g-force acceleration.

Below is the velocity curve for one operation: $$\text{Accelerate outbound payload:} f(a) = t_0 \rightarrow t_1 \\ \text{Release and reverse direction: } f(b) = t_1 \rightarrow t_2 \\\text{Catch and decelerate incoming payload: }f(c) = t_2 \rightarrow t_f$$

(Velocity curves are not drawn to scale and are not required to be linear)

I need to make the sum of these acceleration curves $f(a)+f(b)+f(c)$ as short as possible, while preventing unreasonable forces on the crew. So the acceleration constraints are:

• Acceleration through $f(a), f(c)$ can be no more than 1.2g

• Acceleration through $f(b)$ should remain at 1.2g for most of the time, with no more than 1-hour bursts at 2g (possibly at night time when everyone is lying down, with forced oxygen masks)

• Grant 2 weeks exposure to microgravity at each crew swap (expecting this twice per tour of two hauls).

What is the shortest duration for this trip $t_0 \rightarrow t_f$, and could a physically fit crew do this job twice per year without known physiological injury?

I am also curious what time dilation differences this crew would experience each flight

Answer 1

If you fall back to Newton, then $t_0-t_1=t_2-t_f$ ((de)acceleration) = 30 days, $t_2-t_1$ (reverse) = 55-60 days (60 hours of +0.8g would not save much time, but can be used to correct interception course). Total is about 4 month (we need time for manuvering and rest). Since max gamma factor is only $\sqrt{1-0.01} = 1-0.005$, relativistic effects would give you less then a half of a day dilation and we can keep to this classical numbers - the error would be less than approximations we took.

So you can do up to 3 jobs in a year

1g is a huge acceleration!

P.S. at low relativistic speeds it is sometimes simpler to calculate in classic and then bring relativistic corrections. Wich can be easely calculated using approximation formula $\sqrt{1-x} = 1-x/2$

Answer 2

ksbes answered the core part of the question, but I'd like to reframe it slightly to show how terrible the idea is.

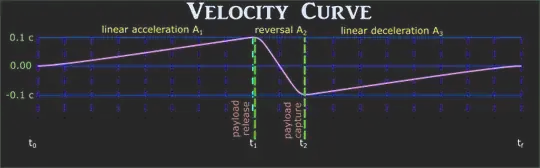
Your tugs, mass $m_t$ need to push a barge, mass $m_b$ up to .1c, and decelerate a second barge down from .1c. They also need to reverse their velocity vector in between, slowing down their own mass to a velocity of 0 relative to their starting point and then back up to .1c again. If the tug did the trip on its own, it would need a $\Delta_v$ of 0.4c. Generally speaking, you don't want a $\Delta_v$ greatly in excess of your rocket's exhaust velocity, and the only thing with an exhaust velocity that high is a beam core antimatter rocket (we'll ignore the implausibility of such a rocket for now) with a $v_e$ of about 0.33c.

Working backwards, the braking $\Delta_v$ will be 0.1c, with a mass of $m_t + m_b$.

Now, A gentleman named Robert Frisbee did an interesting paper on beam-core driven starships (How to build an antimatter rocket for interstellar missions) where he observes that the normal delta-V equations don't apply to antimatter rockets, because a load of the mass involve simply up and vanishes (or rather, turns into deadly gamma rays, but one problem at a time). Instead you have to use a different equation to compute the mass ratio of your ship:

$$k_1 = \sqrt{(1-a)^2 + 4av_e^2 / c^2}$$ $$k_2 = (-2v_e*\Delta_v/c^2) + 1-a$$ $$R = \left(\frac{(k_2-k_1)(1-a+k_1)}{(k_2 + k_1)(1-a-k_1)}\right)^{\frac{1}{k_1}}$$

where $a$ is the proportion of mass flying out of the back of your rocket compared to that going into the reaction chamber... Frisbee's antimatter rocket had $a=0.22$. Anyway, this gives a mass ratio the boost and brake phases of 2.55 (eg. the fuel mass is 2.55 times the dry mass of the tug and barge). The non-beam-core mass ratio equation would give more like 1.35, so you can see already that things are starting to get awkward.

The braking phase needs a propellant mass of $m_{p3} = 1.55(m_t + m_b)$. The turnaround phase needs a $\Delta_v$ of 0.2c, and so a mass-ratio of 4.44. It needs to push the propellant used for the braking phase too, giving a a propellant mass of $m_{p2} = 3.44(m_t + m_{p3})$. The boost phase needs a $\Delta_v$ of 0.1c, and it needs to push the barge and the rest of its fuel, giving a propellant mass of $m_{p1} = 1.55(m_t + m_b + m_{p2})$. This gives a required initial mass ratio of $16.1466m_t + 10.8146m_b$. Lets say the tug is 100 times smaller than the barge. This means that for every tonne the barge weighs, you need nearly five and a half tonnes of pure antimatter. And that's not even per tonne of cargo, because there's the hull of the barge, the shielding, the navigation, the manoevering and docking systems and all the rest! Oh, and building a ship with a mass ratio that high is an additional tricky engineering task, especially when you're talking about antimatter confinement!

This is worse than simply strapping a suitable antimatter rocket to the barge and letting it boost and brake itself, because you're wasting fuel on your tug. The $\Delta_v$ for the barge alone would be just 0.2c, and with a mass ratio of 4.44 you'd need only about 1.72 tonnes of antimatter per tonne of barge!

If you used a single antimatter rocket to do the boosting, and a combination of magnetic parachute, solar sail, sail beam or other non-rocket-based braking system, you immediately reduce your propellant cost-per-launch to a little over a three quarters of a tonne of antimatter per tonne of barge, plus whatever the power requirements of the braking system are (which can be done with solar or fusion, as seems appropriate, which will be cheaper, simpler and safer). Hell, maybe now you can use your beam for the boost phase too, and avoid the whole dangerous business of mucking about with antimatter.

Now there's no tug, there's no need for human crews to spend months and months in a tiny tin box at dangerous speeds strapped to many, many tonnes of a hideously unstable propellant where any one of a thousand little problems will vapourise them in an instant. No maintenance of tugs. No need for rescue operations to retrieve the crew if anything goes wrong (you were gonna do that, right?).

Over seven times cheaper per launch (or more, if you have a beam launch), vastly safer, no miserable crew. What's not to like? And even if you don't like it, you risk someone else setting up this cheap safe alternative in your place, and then where will you be?

Answer 3

In the book The Three Body Problem 2: The Dark Forest, writer Liu Qixin details a kind of oxygen rich liquid that would enter a person's lungs and thus minimize the effects of acceleration. If we assume that this liquid has flooded the ship and that the crew is trained to withstand high g situations, we can estimate that the crew could withstand almost 50g of constant pressure, while it would feel like 1.5g inside the liquid. A quick back of the envelope math suggests that the acceleration and de-acellaration would both take around 17 hours. If an extra 2 hours is required for both launching and receiving the pods, the whole operation might take around 72 hours or 3 days whist not causing any physical damage to the crew.