Mountain sized colossal animal--could it survive, and could it move it's body around?

Question

The question is in the title, but I have bolded the main details to reality-check. I hope that makes it easier to read.

Details: I had the idea of a fantasy/sci-fi animal that never stops growing, and is incredibly long lived. I was playing around with the idea of a cold blooded animal in an extremely cold (say, about -40 Celsius) environment. I'm of the opinion that after a certain amount of growth it and at such cold temperatures, it will inevitably lose the ability to walk around, though for the sake of the story lets say that its muscles do not atrophy, like those of polar bears, and that given the right circumstances, it could begin to slide its massive way across the tundra.

It has a heating organ that produces heat in response to the animal eating food; the increased heat stimulating growth. There is a civilization of humans who ritualistically feed these creatures over 100s of years until they grow to be the size of mountains, which shelter their human villages from the cold.

Can you see any physical limitations that cannot be overlooked when designing such a beast?

As an idea of where this is going, say that as human society advances, global warming or a nuclear disaster increases temperatures in the area and these huge creatures the size of mountains awake. Then, through a combination of organic compounds produced by their bodies which sublimate and become volatile/flammable at temperatures above -20 Celsius, and the excessive heat produced by heating organs which never evolved to turn off, these colossal fire-breathing mountains (i.e. dragons) wreak havoc on an unsuspecting humanity.

Answer 1

This is the nth time I'm using this image on the site. I could not find a specific question to point you to though. Just remember that the square-cube law is a cruel mistress: every time your creature height or length doubles, if other measures scale proportionally then its surface area quadruples and it volume increases 8x. Even when they are able to stand, the larger the creature the more solutions it needs to disperse heat. So on top of being too large your creature would die from fever even without the heat organ.

(Source)

Answer 2

Let's make some assumptions on the shape of our animal first:

• It is roughly mountain shaped, so a flat cone. To get a good base area, it's radius is about 3 times its height.
• It propells itself over the frozen wastes by resing on a hard shell of bone on the underside, using stumpy appendages to push itself over flat, frozen land at almost glacial speed.
• It has some sort of vision to allow navigation by seeing where it is flat.

Shape

Cone-shape has one large benefit: we put the weight close to the ground and give it a rather good weight distribution. The lowest layers of the beast turn into bone or similar calcified material. The thickness of this armor increases with age but it also gets used up by using over rough terrain to some degree.

The base area of the moving mountain would be $A=2\pi r$ while its volume is $V=\frac 1 3 \pi r^2 \frac r 3=\frac 1 9 \pi r^3$. That is somewhat more favorable than a spherical shape. Now, there are three limits to our creature's size: What can be fed (which is hard to calculate), what the floor can carry and the point where it doesn't seem to grow anymore.

Shatter the earth?

Let's look at what the ground can carry. We know the area it rests on and assume an average density of 1 t/m³ for the creature, making it technically the same as water (but simplifying the math a lot: $M=V\times\frac {\text {t}} {\text {m}^3}$). Assuming the ground is basically made from Ice of about a kilometer thickness ($d=1\text{ km}$), then we can use Gold's Formula $P_{\text{min/max}}=B\times h^2$ for the maximum load of a square meter of ice. h is the thickness of massive water ice, and would be adjustet down to half for ice that was formed by compressing snow. Let's assume $h=\frac 2 3 d$. B is a factor that is between 3.5 and 5, incorporating the safety margin and the pureness of the ice. That gives this graph:

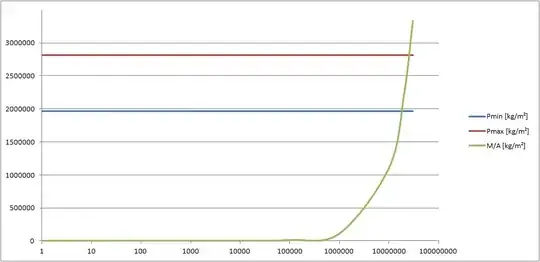
The X-Axis is radius in meters, displayed Logarythmically, while the Y-Axis is the load per square meter. The green line crosses the lower safety margin P_min at about 1968.75 tons per square meter. By working with the formula a little, we get $R_{\text {min/max}}=9\times P_{\text {min/max}}$, or R_min=17718750 meters and R_max=25312500 meters.

This gives our beast a maximum diameter of about 35437.5 kilometers before the ground starts to break under its weight. That would mean our beast would pretty much engulf half of the world, so we can assume that the ground stability is not a practical limit for our beast.

does it still GROW?

Now, we want to see when it doesn't seem to grow anymore. When does it grow? Well, it grows if the radius or height are still noticeably increasing. Assuming we manage to feed it consistently so that there is a linear increase in volume, when does that ebb off in growth of radius? Well, $V=\frac 1 9 \pi R^3$ and then some math magic... and we get this: $R=({\frac V 9})^{1/3}$.

Let's make an estimation about volume increase by age. Let's say beasts start with 1 m³ of volume. They at first grow with a factor that is linked to its age. How about... they quadruple their volume each year for the first 9 years (to get a sizeable 30 m Radius at age 9), then their growth slows down to a linear volume increase per year. Let's say 10000 m³ per year. Which gives us a growth pattern in radius like this: X is age in years, Y is radius

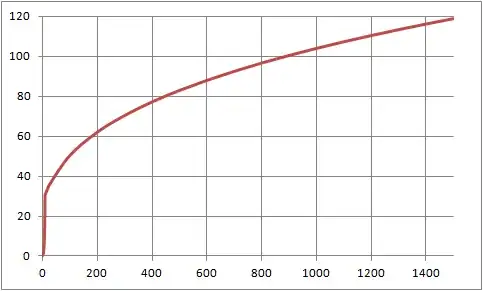
That's much easier to read from: it takes our beast 10 years to get to 30 meters radius. Then 6 generations to reach double its size. Another 9 generations get it from 60 to 80 meters radius, 15 more to get from 80 to 100 meters radius, and 18 more to grow from 100 to 120 meter radius.

Speed?

Now, where is the point the beast becomes stationary? Well, THAT is fricion versus power. Friction is a breakign force that goes linear to a coefficient and the normal force, which in our case is simply the weight force. $F_f=\mu F_N$ where $F_N=M*g$ and $\mu ~ 0.02 \to 0.09$, assuming the lowest layer of the beast is actually ice clinging to the porous boney sponge.

That is a REALLY low friction, so let's plot it and assume our beast manages to apply. Let's assume it has some kind of limbs along its circumference and that they can create about 100 Newton of forward force per meter of circumference. That is a simple plotable thing! $C=2\pi R$ and a resulting forward force of $F=F_l-F_f=100*2\pi R - 0.05 \times 9.81 \times \frac 1 9 \pi R^3$. For what R does this equal to 0? That's the point our beast has to halt and rest forever. Let's simplify first... $F=\pi (200 R - 0.0545 R^3)$ And now plot the two parts against each other!

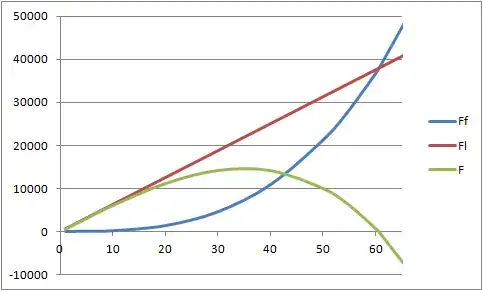
The forward force becomes very close to 0 at 60,57825 meters radius. A tiny bit more ant it is negative, meaning it will stay stuck, a little less and it can still slide ok. In other words, up until about 35 meters radius, it is perfectly mobile and gets faster and then starts to slow down until 60 meters, which is the point it will have to find a resting spot and further growth is only possible by being fed exclusively.

120 meters diameter (which is the 200-year marker from earlier) is not a mountain, but a sizeable hill, but we can increase the strength per meter of circumference to stretch it.

If we assume that each meter can push tenfold, we get tenfold the radius. 1.2 kilometer diameter and 400 meters height is a small mountain, so perfect! Each meter of circumference just needs to be able to push as half a strongman (1000 N ~ 100 Kg), so for a strong beast, we might even manage 2.4 kilometer diameter. But when does it reach this diameter?

150000 years give us a 550 meter radius, so 1100 km diameter. 900000 years give a 1000 meter raius, which is 2 kilometers diameter. And after 1.55 million years, one of these beasts finally reaches its critical size and has to find a resting spot.

The heat problem

Now, it is a gigantic mountain. How do you get rid of the heat that is generated by the various processes and keep the beast stable? Well, we have resorted to calcifying the lower levels of the body to a good degree already, why not use calcifying parts further up in the body too? Our moving mountains could create large air-tubes that reach down to its inner core, venting the heat outside. Due to temperature differential, some of these pipes, some meters in diameter on an adult beast, would exhaust air while others, closer the the bottom, would, as a result, suck in air. It would be a pure convection stream, and could be enough to supply the beast with the oxygen it needs, provided that the airspeed is high enough.

Because of the temperature of the permanent exhaust - let's say 30 to 40 °C - it would flimmer in the -40 °C winter air, creating theillusion of permanently breathing flame...

A village might settle on the back of an old beast and divert some of the permanent exhaust to power simple machines or heat their houses.

Final conclusion

A moving mountain is feasable in the regards of ground stability and the ability to push itself around within some limits. It also is feasable in the reagars of not seeming to die from age, given some constraints that push the point where one of the beasts gets stuck. However, I can't solve the problem of how much food such a colossus of a beast would need to move, even glacially slow. I can only estimate that the beasts would probably die from hunger before they are locked into a specific position by their weight alone.

Problem mitigation

Some problems might be solved if the beast is not one singular being but actually somethign like a coral reef. The whole internal heat would be no problem then, as the whole being only has a living outer shell while the internal structure consists entirely of dead matter. It would need some two specialized forms though: one that makes up the pushing legs and one that makes the top of the mountain.

Answer 3

You're not going to wind up with anything like a dragon because the square-cube law is a harsh mistress, but if you're creative you might be able to make a giant creature, of sorts.

The square-cube law is a lot less problematic if your creature is relatively flat, and no single part of it is unreasonably thick. Say, for instance, a giant starfish-like creature with the height of a dinosaur and the area of a small hill. A giant snake or centipede will also work, you can make it arbitrarily long and it shouldn't have a problem with being crushed under its own weight.

However, then you're dealing with a different problem - getting oxygen and nutrients to all parts of its body at once. There's a limit to how much a creature can eat or breathe through a single hole, and the bigger the creature is relative to that hole, the more it's going to need to keep itself running. Nervous systems also have a limit on how fast signals can travel, slowing reaction time, and there is a limit to how much blood the heart can push. This can be "resolved" by putting mouths, brains, and hearts all over its body, and giving it hundreds of digestive, respiratory, nervous and circulatory systems.

However, at that point you're dealing with a bigger question of why such a creature would exist. It's less efficient and less capable of feeding or defending itself than an equivalent herd of more reasonably sized, individual creatures (it's basically a herd of dinosaurs stuck together), so it wouldn't evolve naturally. You've answered this somewhat by saying that humans are responsible for feeding, defending, and possibly breeding it, but if you have enough food to keep such a colossal creature alive, there are far simpler ways of turning biomass into heat than a mountain-sized living furnace (like feeding regular-sized pets or livestock - snuggling with their sled dogs is a time-honored tradition for arctic explorers - or just burning it).

Answer 4

According to some experts if land animals weighed the same as blue whales (180 tons) they would apparently be too heavy to move around and would collapse under their own weight.