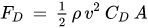I have a superhero setting where one guy, when fully powered up, is a flying-brick type with energy blasts who I think of as being able to lift about 1000 tons (about 10 million Newtons), and this lifting power translates directly into flight. Now, the superpowers in this setting are basically magic, coming from a source outside of the laws of physics. That being said, as defined right now, this is a potentially world-busting power. If the only limitation to his flight/lifting ability is '10 million Newtons', then the amount of power he can generate is arbitrary. He could simply fly directly away from earth at an acceleration of about 100km/s^2 for a few days, come back at relativistic velocity, and hit with the energy of the Chicxulub asteroid. This would be bad, for several reasons.
I think it would be more convenient for me to think about his capabilities in terms of power generation. To pull a ridiculous number out of the air, say that his personal peak power generation is about 75 GW, about 5% of the U.S.'s total energy consumption. That enables me to figure out how much destructive power he can output via his energy blasts, but there's no way to directly convert this into force, making his lifting strength and flight acceleration arbitrary.
So, I figure that I'm giving him a specific power output (75 GW, generated via magic nuclear reaction), and his flight works by telekinetically 'pushing' against every atom within a 1 km radius of himself, and equivalent force is applied back to him, satisfying 'every action has an equal and opposite reaction'. If he's in the air, that's a little over 4 billion cubic meters of air, and air density at sea level is about 1.22 kg/m^3, so let's assume that he's pushing against 4 billion kilograms of air.
What equations do I use here to determine his flight acceleration, or how much he can lift? By how much does he push the air around him? I can use the rocket equation and kinetic energy equations to figure out how much acceleration a spaceship can get, but I don't think I can apply them here.
EDIT: Also, let's assume that the guy masses 100 kg, just so we have nice round numbers.
EDIT2: To clarify, telekinetically pushing against an object in his area requires as much energy from him as is determined by the kinetic energy equation (1/2mV^2), the same way that expelling reaction mass from a rocket requires, at minimum, the kinetic energy imparted on the reaction mass to give it its speed.