Hot rods into space!

Question

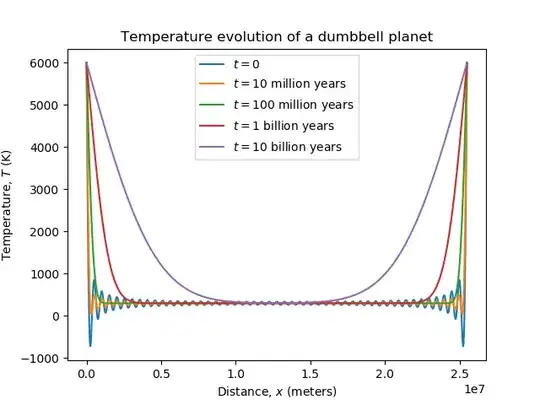
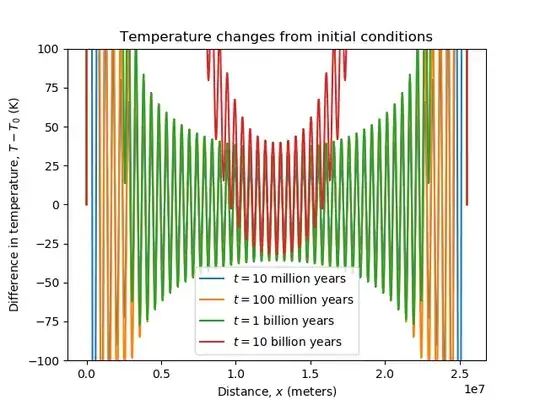
Based on this question about an impossible barbell planet, how hot would the bar be if it extended from halfway in the Earth's mantle to an altitude of 2r of Earth's radius? The diameter of the bar itself is 20% of the radius of Earth. The rod is made of mild steel (we are handwaving the structural integrity of molten steel and ignoring that a structure this high would instantly collapse.) Also, the rod is permanently affixed at halfway through the mantle. The orientation and distance between Earth's core and the bar are fixed points.

We are going to ignore orbital mechanics, structure strength of megastructures, and structural strength of the Earth's crust surrounding this megastructure.

Given the Earth's core temperature and the conductivity of mild steel, how high would a person have to go on the rod in order to touch the rod with their bare hands and not get burned?

Bonus Question(s): What would happen to the weather near the base of the rod where it intersects with earth? If you want to talk about how fast Earth's core would completely cool off, that's cool too.

Extra Bonus Question(s): Account for orbital mechanics, interaction with the magnetosphere, and compression heating of the rod against the earth's core and friction with the crust.

Remember, this is a hard-science question. Equations, official government sources, and journal references are most appreciated. A minimum of handwavium, please.

Answer 1

As a first approximation, we treat the rod as a one-dimensional rod of length $L$. On each end is a heat source (the mantles of each of the two "Earths". We can begin to model the system as following the one-dimensional heat equation: $$\frac{\partial T}{\partial t}=k\frac{\partial^2T}{\partial x^2}\tag{1}$$ where $T$ represents temperature, $x$ is the distance from one end of the rod, $t$ is time and $k$ is a constant, the thermal diffusivity. Consider a case with the following boundary conditions: $$T(0,t)=T_1,\quad T(L,t)=T_2,\quad T(x,0)=f(x)$$ The first condition is because both heat sources are identical. We can use the method of separation of variables to arrive at our solution: $$T(x,t)=T_1+\frac{T_2-T_1}{L}x+\sum_{n=1}^{\infty}B_n\sin\left(\frac{n\pi x}{L}\right)e^{-k\left(\frac{n\pi}{L}\right)^2t}$$ where $$B_n=\frac{2}{L}\int_0^L(f(x)-u_E(x))\sin\left(\frac{n\pi x}{L}\right)dx,\quad u_E(x)=T_1+\frac{T_2-T_1}{L}x$$ In our case, $T_1=T_2$ and $f(x)=T_0$ is uniform. Then, if $\Delta T=T_0-T_1$, $$B_n=\frac{2\Delta T(1-\cos(\pi n))}{\pi n}$$ and $$T(x,t)=T_1+2\Delta T\sum_{n=1}^{\infty}\left(\frac{1-\cos(\pi n)}{\pi n}\right)\sin\left(\frac{n\pi x}{L}\right)e^{-k\left(\frac{n\pi}{L}\right)^2t}$$ Wikipedia cites steel as having roughly $k=2\times10^{-5}\text{ m}^2\text{ s}^{-1}$. Let's say $L=4R_{\oplus}$, $T_1=T_2=6000\text{ K}$ (according to estimates), and $T_0=300\text{ K}$.

It turns out that the bridge between the cores heats up really slowly. I computed the first 100 terms of $T(x,t)$ at a variety of times, and plotted them.

The strong oscillations at the ends are just examples of the Gibbs phenomenon, and don't have physical significance.

It becomes dangerous to walk on the rod after timescales longer than about 100 million to 1 billion years, from what I can tell. The center should remain habitable.

There are a couple of things we haven't considered:

• Radiative cooling, which I think will be important. This also might mean that the ends of the rods - at least, the sections immediately protruding from the surfaces of the planets - could appear quite bright. After all, 6000 K is approximately the temperature of the surface of the Sun!
• The fact that the rod is a cylinder, not one-dimensional. I don't think this is a major factor when it comes to the relevant timescales, though, especially if the rod is thin.
• The ends of the rod are embedded inside planets, and heat will diffuse into the outer layers of the planets. There should also be a non-zero gradient at the cores, at $t=0$.
• Atmospheres have an impact on temperature circulation; the (cooler) sections of the atmosphere around the two planets should take in heat from the (hotter) sections around the rod.

That said, I think this simple 1-D model can give us an order-of-magnitude estimate.