Is it reasonable to use the rate of radioactive decay as a new way of measuring time

Question

The unit of measurement known as a Curie(after Pierre and Marie Curie) measures the rate of decay of Ra-226 in one second. It was originally measured at 3.7x10^10 decays per second. It has been more accurately measured to 3.6x10^10 decays per second.

I want to use the Curie and create a new unit of time measurement. I think if I measure how long it takes the radium to decay 1x10^10 I could create a new "second".

Is this even feasible? Is it reasonable to use this?

My thought process was to try and find a stable system to create a new unit of time measurement from it. It may be more ideal to use the more accurate measurement but I want to see if this is dumb or not.

Answer 1

It depends on the span of time you wish to measure. To measure a short/human scale time, you may struggle due to the inaccuracies inherent in decay.

But if you want to measure 'oh, it happened 10 billion years ago' and aren't sure who will be around to read the clock, then radioactive decay may be a solution.

Uranium-238 has a half life of 4.5 billion years. There is no mechanical or electrical clock that can function that long, but a container can be made that contains 1kg of uranium-238. 4.5 billion years later it will contain half a kilogram of uranium 238 and some thorium, protectinium, uranium 234 and a bunch of other elements in uranium's decay chain. Even if you don't know the initial mass, the ratios of elements tells you how old it is.

Fun fact, the voyager space probe carried some uranium 238 (as pure as we could make it) for exactly this reason - so a potential alien civilization could figure out how long it had been travelling for.

Answer 2

Radioactive decay is nonlinear and the decay products will change the alpha detection rate.

This will not work as an absolute measure because it’s not possible to measure just the radium decay, and over time the decay rate slows down. The rate of nuclear decay depends only on the isotope and the quantity of material present. The number you gave us for the Curie, is the count we would see if you had exactly one gram of Radium-226. The calculation for how much radium-226 you have at any given time is as follows:

$$N = N_o\times\frac{t}{2}$$

Assuming you know that you started with n moles of radium (that will be $N_o$ in the formula); we already know that the half life is 1,600 years, so as time (t) goes on you can see you have less radium. Less radium means slower decay rate. Each isotope has a decay constant (λ) that can simply be multiplied by the amount of the element to find the decay rate at a given time:

$$λ = ln(2) / T_½$$

λ for ²²⁶Ra is ln(2)/1,600 years = $\frac{1.3737112e-11}{sec}$

With that constant in $s^{-1}$ (years were converted to seconds), you can predict how many counts per second you'll have from your radium. If you have exactly 1 mole of ²²⁶Ra, then you will have 8.2330422e+27 counts per second.

Why is that so much higher than your number? Because Radium is pretty heavy. To make one gram of radium-226, you only need 0.004424778761061947 moles of it, or exactly 2.6646641e+21 atoms. Let's try that out in the radioactive count formula:

$$ 2.6646641\times10^{21} \text{atoms} \times \frac{1.3737112\times10^{-11}}{sec} = 36604490741.7 \text{ counts per second.} $$

And that you will recognize is the Curie you referenced.

So there is no precise rate of alpha emissions from a sample of radium-226, the amount of radium you start with determines the rate of decay for the sample. But worse, it is also leaving behind daughter products, which are also producing alpha particles at very different rates. You will be detecting alpha particles from radium, and radon, polonium, and lead all the way down until it becomes stable as ²⁰⁶lead. As time goes on the radium, turning into other elements, will cause the detector to read alpha particles for those other elements, and your rate of detection is going to change. Overall this is a very small amount, and you can make a fairly precise clock using radium 226. But using it as a definition of a unit of time won’t work. When you lock up your block of radium and come back years later to measure it, you can’t reproduce those original numbers exactly. Because, it's no longer pure radium.

So what is it? Radium-226 (1600 year half life) yields an alpha particle and Radon-222. The half-life of radon-222 then is approximately 3.8 days. This means that after 3.8 days, half of the initial amount of radon-222 has emitted another alpha particle and transformed into polonium-218 (Po-218). Your alpha detector will see this and count it as a radon decay. Polonium-218 (Po-218) also undergoes alpha decay, emitting an alpha particle and transforming into lead-214 (Pb-214), and further screwing up your counts. Lead-214 (Pb-214) then undergoes beta decay, emitting a beta particle (an electron) and transforming into bismuth-214 (Bi-214). Beta particles won't register on your alpha detector Bismuth-214 (Bi-214) undergoes beta decay as well, transforming into polonium-214 (Po-214). Polonium-214 (Po-214) undergoes alpha decay with a half-life of approximately 164.3 microseconds, becoming lead-210 (Pb-210). Lead-210 (Pb-210) undergoes beta decay, transforming into polonium-210 (Po-210). Polonium-210 (Po-210) undergoes alpha decay, becoming lead-206 (Pb-206), which is a stable element. So, the decay chain of radium-226 ultimately leads to the stable element lead-206.

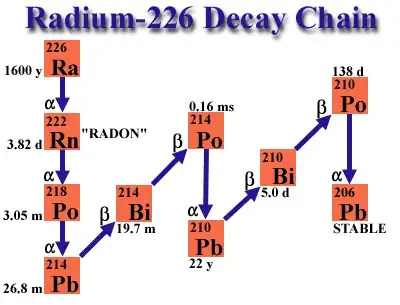
(Decay chain of ²²⁶Ra)

If you were counting, that’s five alpha particles until Radium-226 becomes Lead-206, and only one of them were from the radium. It is incredibly complicated, but as the amount of radium goes down, you will see alpha particles coming out faster because the radon and polonium will be decaying.

This means that over time your initial block of radium will become a soup of several elements and the rates of decay for all of them are very different. Mostly you will have lead and radium at any given time since they linger longer. But as your radium turns into other stuff the rate at which alpha particles will be detected in any given second over time will constantly change.

Now to further confuse the problem, this isn't all guaranteed. I said that beta decay won't mess up your count, but that's not entirely true. ²¹⁰Polonium has two other modes of decay: beta capture and spontaneous fission. When ²¹⁰Po captures a beta (electron), it turns back into ²¹⁰Pb. Now, ²¹⁰Pb can also emit an electron in beta decay to become ²¹⁰Bi, which in turn can create another alpha particle to return to Lead 208.

While you can keep very accurate time with a sample of Radium-226 for short intervals, it’s not something that would make a practical standard unit of measure.

Answer 3

Yes, you can me. But it is impractical. The decay of Radium-226, and any other radioactive element, is exponential. It slows down as more of it decays. So you can’t do simple math to figure out how many milliseconds would have passed if 1x10^10 decays occurred.