This has indeed been investigated. I found a thesis by Daniel Jontof-Hutter (2012) that did a stability analysis of particles in rings orbiting, among other bodies, Saturn. One important quantity he studied was the ratio of electric force to gravity, $L_*$. When $L_*\gg1$, the electric force dominated (the "Lorentz regime"), while when $L_*\ll1$, the gravitational force dominated. The exact value of $L_*$ determines whether the rings will be stable or not; the presence of the electromagnetic field can lead to instabilities. There's not an analytical stability condition, unfortunately, so we have to look at numerical simulations to answer your question in full.
Technical details
Jontof-Hutter considered the Lorentz force in the case of a rotating magnetic field:
$$\vec{F_B}=\frac{q}{c}\left(\vec{v}-\vec{\Omega_p}\times\vec{r}\right)\times\vec{B}$$
where $q$ is the charge of the particle, $c$ is the speed of light, $\vec{r}$ and $\vec{v}$ are the particle's position and velocity, $\vec{\Omega_p}$ is the planet's spin vector and $\vec{B}$ is the magnetic field. The electric component of $\vec{F_B}$ is $q\vec{E}$, where $\vec{E}$ is the electric field:
$$\vec{E}=-\frac{1}{c}\left(\vec{\Omega}\times\vec{r}\right)\times\vec{B}$$
$\vec{B}$ is given, for a dipolar magnetic field, as
$$\vec{B}=\frac{-g_{10}R_p^3}{r^3}\vec{z}$$
where $R_p$ is the radius of the planet, $r=|\vec{r}|$, and $g_{10}=|\vec{B}(r=R_p)|$. Therefore1,
$$L_*=\frac{qg_{10}R_p^3\Omega_p}{GM_pmc}$$
where the planet's mass is $M_p$ and the particle's mass is $m$.
Let's go to a picture. 16,000 grains were simulated, at many different values of $\vec{r}$ and $L_*$. Here are the results:
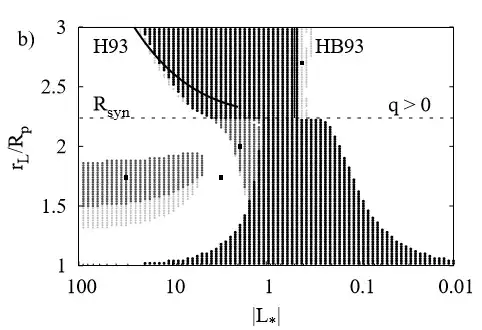
The darker the dots, the more unstable the configuration. Here's an annotated version of the diagram:
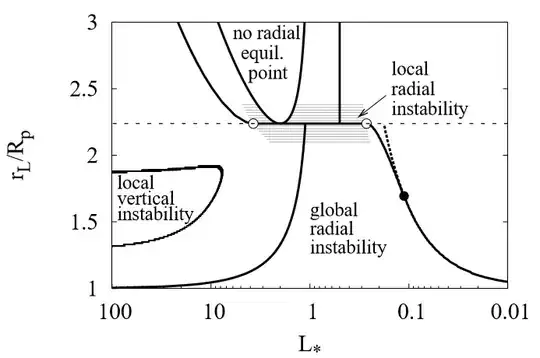
$R_{\text{syn}}$ is the radius at which an orbit is synchronous with the planet's rotation. Essentially, at small $L_*$, the rings should be stable at almost all radii. In regimes where $0.5<L_*<10$, there are fewer stable regions, and you can't have large stable rings. This does become less of a problem with large $L_*$, but there are still instabilities, more than for $L_*\ll1$.
1If you want, you can view this as
$$L_*\propto\frac{\Omega_p}{Q\bar{\rho}_p}$$
where $\bar{\rho}_p$ is the mean density of the planet, and $Q$ - notation I've absolutely butchered - is the mass-to-charge ratio of the particle, $m/q$.

