Are genetically engineered wyverns with my specifications possible?

Question

In my post-apocalyptic iron age world meant to be a sci fi twist on fantasy tropes, wyvern like creatures simply known as fliers were said to have been originally created by a crazy billionaire as a gift to his son, but later modified by bioterrorists to instill fear in the population.

Some things to note:

• They are considered reptiles, but are actually warm blooded as it's theorized some dinosaurs were.

• DNA from many different sources, namely a large variety of mammals, birds, and reptiles.

• Wild dragons are even more rare than captive ones. Genes inserted by the interlopers have become dominant over the years.

• Cannot breathe fire but the bioterrorist genome added the ability to spit venom. While it is most likely just blinding, similar to a cobra's, I'd like some insight as to if it's possible for victims to get chemical burns from an animal's venom, hence the bombardier beetle DNA.

• Typically they grow to be slightly larger than a horse, just the right size to ride comfortably.

• Can fly, but adheres to laws of both biology and physics. Requires open space to take off. Fully grown individual can usually fly between 6 and 8 hours on energy alone, longer if there is good wind. Requires high food intake to fly.

• Need some insight on their bones. Hollow avian bones would reduce the weight, but are easily broken by a human rider. However, conventional full bones of other animals might be too heavy.

• Usually found in various shades of browns, grays, oranges, and greens. Black is often a sought after color as it's believed those dragons are healthier. A very recessive gene originating before the fall of civilization is the color changing skin granted by optional chameleon DNA, which cost an extra million on the customization website.

What I need to know is how long is the wingspan required to fly, and several other questions listed above.

Answer 1

The largest known flying animal which ever lived on Earth belonged to the Pterosaur family. They came in all kinds of sizes, but some of the largest sub-species had wingspans of over 10 meters. It's hard to tell how heavy they were from fossil evidence alone, but most paleontologists assume that in spite of their impressive size they weighted only a few hundred kg. Still, with the right genetic enhancements, carrying the additional weight of a human seems plausible.

Note that riding a bird might be different than riding a horse. First, it would be important to be near the center of gravity of the animal, and that would usually be just between the wings. Second, aerodynamics are far more important. So the ideal riding position might be laying down, not sitting upright.

Answer 2

To be able to fly, the wyverns would need more than just a large wingspan. For example, a human would need a wingspan of about 6.5m to be able to fly, but humans do not have enough body strength to be able to support wings of such size. (See here for more information from Yale: http://www.yalescientific.org/2013/03/qa-why-cant-humans-fly/).

Basically, birds have air sacs connected to their lungs, which makes it easier for them to pass oxygen through their body during flight - plus the hollow skeleton, which reduces the weight they have to lift with their wings.

If an average human (say, 65kg) needs 6.5m wings to fly, an average horse (of anything between 300kg and 1,000kg) would need to generate a lot of lift, and have an adequate strength-to-weight ratio in order to actually have functional wings. Somewhere between 10-20m would be enough to (theoretically) lift a horse, and the wings may require a number of elbow joints if you want the wings to be able to fold.

I'm less sure about the bone structure required, but if the musculature of your wyverns is strong enough, you wouldn't need hollow bones to make them lighter; they'd just need to be stronger to compensate.

Answer 3

A wind is not going to make flying easier. It makes taking off easier, but that is it. Flying is relative to the air. So, wind may boost or lower your speed versus the ground, but it doesn't affect flying once you are airborne.

Soaring is probably possible. It is actually possible for a very strong Bicyclist to get airborne and remain airborne by pedaling. http://www.telegraph.co.uk/news/newstopics/howaboutthat/10177573/Bicycle-powered-helicopter-wins-Canadian-inventors-250000-prize.html

Of course, gliding/soaring itself isn't a problem given the popularity of hang gliding.

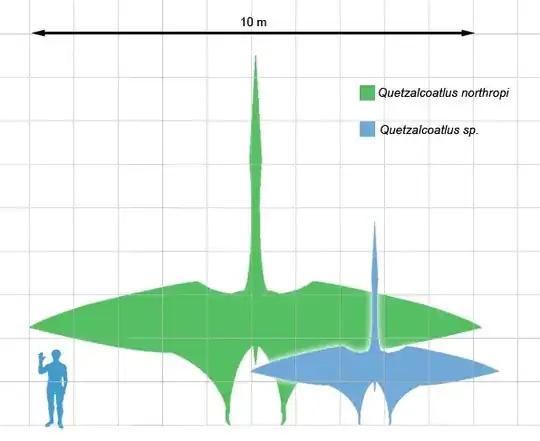
Aspect ratio is the ratio of the length to width of a wing. An albatross has an aspect ratio of more than 10:1. High aspect ratio makes for a more efficient wing. Increasing the aspect ratio reduces the sinking speed of the wing when soaring. In terms of wing loading, N/m2 large birds are in the 75-100 N/m2 range.

Let's say the beast has a weight of 150kg (or 330lbs). There are 9.8 N/kg. Let's call it 10 N/kg for simplicity. We have 1500 N. 1500 N divided by 75 N/m2 equals 20 m2. If we approximate the wings as rectangles (which they wouldn't be all the way to their ends), 10x*x=20m2 is their area just to get this airborne let alone with a rider. x=1.42m. That is a wing width of 4.65 feet at the wing's base and a wing length of 46.5 feet for both wings together or 23.2 feet per wing. That is unmanageably long.

Of course, soaring alone (which is what fixed wing aircrafts do) is not enough. Powered flight by flapping is required at least occasionally. Birds usually create small puffs of air they force downward with each stroke. These are discrete cylinders of downward moving air when the bird is moving slowly, and the cylinders start to overlap and run together when the bird is flying faster.

Assuming we somehow get around the muscle strength issue, there is an addition problem: the Reynold's number. This is a dimensionless number that describes how reality change as you scale up or down in size. Air moves smoothly over streamline bodies until the Reynolds number hits about 2,000,000. Air moves smoothly over non-streamlined bodies (such as the body of a rider) until a Reynolds number hits about 200,000.

Once you are above this cutoff number, air starts to move chaotically around the flying object. Drag is doubled, and eddies (turbulence) form. Basically, it is not at all clear whether it is possible to reliably push a significant quantity of air downwards in the direction you want it to go while air is moving around the flyer chaotically.

It is really hard to study the reasons why something isn't possible, but I looked a while back during my own research. I couldn't even find robots that were able to flying by flapping their wings above this cutoff. It isn't even a matter of being stronger than normal animals.

An albatross with a streamlined body of length 1 meter long flying at 15m/s has a Reynolds number of about 1,000,000. The Reynolds number is proportionate to speed and length of the flyer (so take the 1,000,000 number and multiply it how much longer and faster you want the creature to move). The creature we are talking about is 2 meters long at a bare minimum (the wing width is 1.42 meters without a rider). So, we are talking a Reynolds number of 2,000,000 at very least without a rider and flying very slowly in ideal conditions with ridiculously long wings. So, barely flying by flapping regardless of its strength.

Make the wings bigger to accommodate the weight of a rider plus riding gear and plus the weight of stuff you might want to carry with you, and this reptile isn't flying. Also, the rider reduces the Reynold's number cutoff simply by being non-streamline and so probably doomed the endeavor right out of the gate.

The larger pterosaurs didn't necessarily violate this limit. We don't know if they could do powered flight at all or what weight they were. There are even questions surrounding their supposed wingspan.