8

I want to get a shuttle from place to place in a reasonable amount of time.

Say, 6 to 8 hours maximum, with a short break at the midpoint to turn around.

Assuming constant acceleration to midpoint and constant deceleration after that, what's the highest g-force I could sensibly inflict on my passengers without breaking them?

I'm assuming that they're seated (or lying oriented in the most sensible way, etc) and strapped in throughout the journey.

piersb
  • 181
  • 5

5 Answers5

7

This article talks about NASA experiment with increased g loads.

Summary: they run 22h sessions the subjects were supposed to spend in a centrifuge, this included standing up every 4 hours. The writer of the article ran the session at 1.25g (with some dangerous medical situation). The guy before him managed 1.5g, but got ill at the end. It's not clear how much of the problems was because of the gravity and how much because of the Coriolis force.

Radovan Garabík
  • 14,297
  • 2
  • 25
  • 55
7

NASA Technical note D-337, Centrifuge Study of Pilot Tolerance to Acceleration and the Effects of Acceleration on Pilot Performance (1960) pages 30 and 31 graph G-force tolerance over periods of time. These are the limits where the pilots can still function. They all show a clear downward trend over time.

NASA Technical note D-337 - Figure 10

The longest period of sustained G-force evaluated in the study is ~35 minutes at ~3.5 Gs in the less favorable "eyeballs down" position (ie. deceleration).

NASA Technical note D-337 - Figure 7

These provide an upper bound for tolerance. When extrapolating to 8 hours, please note the scales of the graph are logarithmic.

Schwern
  • 30,166
  • 4
  • 76
  • 118
  • 2
    Extrapolating to 8 hours, we get $g \approx 3.8g$. Extrapolating to one year, $g \approx 2g$, and to 70 years, $g \approx 1.4g$ :-) (of course, the numbers are completely disconnected from the reality at these ranges). For the record, I got from the linear interpolation in the log-log scale the equation $g = 2^{-0.0864 log_2{t}+2.69}$, where $t$ is time in minutes, and the {inter,extra}polation goes from the most favourable curve ("greatly reduced performance"). – Radovan Garabík Oct 05 '15 at 07:21
2

No-one has yet mentioned the possibility of an acceleration tank. If a passenger is immersed in a strong rigid tank full of liquid with pretty much the same density as human tissue, the effective G-force is reduced to one depending on the difference in density between the liquid and the human tissue. We're mostly water, so water is a good match. Bones are denser, but bone and bone connective tissues are tough because that's their purpose. Lung tissue is probably the most vulnerable - it can't be filled with water, because we have to breathe air, and it's delicate. Shockwaves from large bombs kill by rupturing lung tissues.

But do we have to breathe air? There are chemically inert chloroflourocarbons which can cary a large amount of dissolved oxygen. A rat can be submerged in such a liquid and can "breathe" it for a considerable time. I don't know whether it's been tried on humans (and if it has it may be classified secret). An emulsion of such a CFC in saline has medical approval as an emergency blood substitute for when no compatible transfusion is available.

Anyway, I'd guess at something like 10G breathing air in a water tank and maybe up to 50G breathing an oxygenated CFC liquid.

The weight penalty for an acceleration tank is very considerable (many times greater than a passenger or pilot), so the idea has never been practical in aviation or spaceflight. However, if there's a very cheap source of energy for propulsion, maybe it could then become practical.

nigel222
  • 11,701
  • 21
  • 33
1

Making a planet habitable for humanoids: The planet

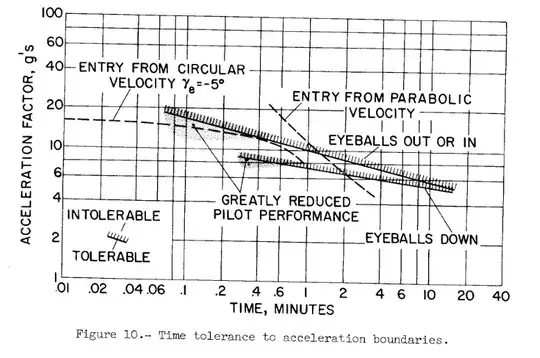
I put a small section in there on G-forces. Orientation is VERY important, some humans can handle up to 45Gs for short periods of time if they're positioned correctly (eyeballs in/on their back - heart-brain same level, spine supported, etc). Vibration is important too. If you're at the wrong frequency even low levels of extra G can be incredibly harmful. If this is a shuttle, and you've got your humans in cradled seats, properly oriented - then you can get a lot more out of them, than say fighter pilots, who experiences jerks, and turns - instead of being correctly oriented to the thrust axis.

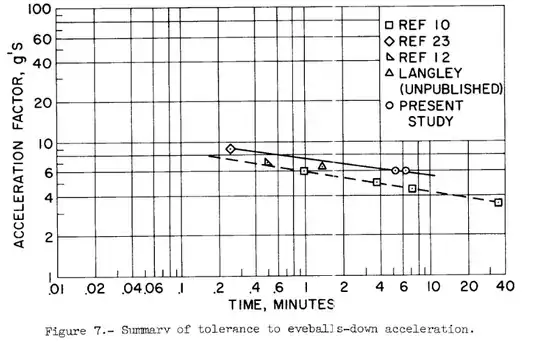
6Gs are handled for something like 10m; because you can only handle 10G for around 1m.

I'd guess a maximum of somewhere around 2G sustained for the 8 hours you're specifying (I don't think anyone has ever had the opportunity to test that duration, much less get us some type of average). And this wouldn't be halfway pleasant at all.

I think if you're launching from the surface of a planet/gravity well, you're going to want to vary the thrust. A lot at the beginning, then give the humans a break, then go into a constant-sustained thrust regime. A lot of thrust, quickly will get you out of a gravity well, whereas lower thrust will take a lot longer to get you a smaller distance - depending on the technology, obviously.

Of course this is going to be some near-magic technology you've got going on, as keeping that much thrust going for that long is difficult - 90% of a rocket's mass is propellant, and we've never done a SSTO. Easier to drop engines after use than to deal with complexities of different thrust needs. And you burn most of that within the first 2m30s (for the shuttle).

Most rockets only burn at lift-off around 1+0.3G to sometimes 1+0.6G, because of engine-scale, etc. Which seems wasteful, as the longer you're in the gravity well, the more you've got to burn just to stay even.

Community
  • 1
user3082
  • 6,642
  • 18
  • 31
  • Thank you.
    • Cradled seats (or futuretech equivalent). Would like to know best orientation (seats so acceleration is towards your back? or feet-towards-boosters?)

    We don't need to get out of a gravity well in this situation, so constant thrust is fine (and probably sensible).

    Right now I'm handwaving the the propellant, and likely to continue doing so

     – piersb Oct 04 '15 at 22:33
  • Constant, steady, non-vibrational thrust from behind, pushing you back into the seat; eyeballs cradled in their sockets (or the retina detaches) - heart and brain on the same plane so the heart doesn't have to pump blood against the force. Legs elevated (seated position is fine), so most of that blood pools in the lower body (ie: brain and torso) - that may not be sustainable long-term (ie: hours) but does work over the short-term (ie: benefit). If you've got future-tech, put them in fluid-pressurized tanks or forcefields. Note the fertility loss. – user3082 Oct 04 '15 at 23:25
-4

Fighter pilots get to live through a tremendous 3g acceleration without breaking their bones, when they make sharp turns. Anything above 3.5g is expected to leave permanent damage to bones and sinews. The crew (if trained for space travel thoroughly) might sustain upto 3.5g without undergoing any permanent damage.

Youstay Igo
  • 20,609
  • 44
  • 82
  • Note that fighter pilots are selected based on a number of physical traits, first and foremost of which are height and weight. A six foot 5 inch male weighing 300 pounds is going to have a very bad day when he suddenly weighs 900 pounds. Things will snap. –  Oct 04 '15 at 15:13
  • 2
    Thank you. However a fighter pilot only maintains 3g for a short amount of time. I'm looking for continuous acceleration over (say) 8 hours. Acceleration of 1g is definitely going to be fine. Acceleration of 13g will certainly be fatal. What's the safe (ish) zone? – piersb Oct 04 '15 at 16:41
  • Fighter jets get about 9g and (trained) pilots survive this just fine. 3g is what you'd expect on a rollercoaster (and survive :-)). This is however not sustained acceleration. – Radovan Garabík Oct 04 '15 at 17:33
  • @RadovanGarabik, to say it again - fighter pilots meet certian height and weight requirements. Its also important to note that rate of change and frame of reference are important. The instantaneous change from 0 to 1G will absolutely kill you if you hit the ground from a few thousand feet. –  Oct 04 '15 at 18:33
  • It doesn't matter how much height you fall from when the shock value is determined by g. Some high end racing cars these days hit 0 to 100 km/h in 7.3 seconds or so. I don't know how much that would count in g, but I'm sure it's a pretty high value. – Youstay Igo Oct 04 '15 at 18:42
  • 1
    @SeanBoddy Actually, when a falling person hits the ground they briefly experience hundreds of g's of acceleration. Speed of onset is important, but if the acceleration itself is survivable it mainly affects things like whiplash. – 2012rcampion Oct 04 '15 at 18:42
  • @SeanBoddy Yes, that's why they (fighter pilots) are able to withstand 9g routinely. Normal, healthy adult can survive 3g for minutes without any negative effects whatsoever (again, think rollercoaster). Anyway, hitting the ground does not translate to jerk easily, it's the deceleration (in hundreds of g) that kills you when you hit the ground. – Radovan Garabík Oct 04 '15 at 18:44
  • And it also heavily depends on the micro and macro elasticity of the surface you are falling on. Falling on sand is not the same as falling on concrete. – Youstay Igo Oct 04 '15 at 18:44
  • @RadovanGarabik, indeed. My point is that in a certain frame of reference, as a freefalling body, the victim starts with the experience of zero G and ends with the experience of 1G. I think we essentially understand each other - the OPs vessel must not instantaneously accelerate. –  Oct 04 '15 at 18:51
  • 2
    @YoustayIgo 100 km/h in 7.3s is a regular consumer car. Bugatti Veyron is about 2.4s. Anyway, assuming constant acceleration, $a=2v/(t^2) \approx 1.1 ms^{-2}$, or about 0.11g. Hardly noticeable. For the Veyron, it's 9.6 $ms^{-2}$, or 0.98g in addition to Earth gravity, but it's perpendicular, so the total g in Veyron would be about 1.4g. – Radovan Garabík Oct 04 '15 at 18:57
  • Good point reminding the two points of references in this scenario! I think fighter pilots would feel the same when taking horizontal curves. – Youstay Igo Oct 04 '15 at 19:01
  • 1
    @SeanBoddy Yes, I think we understand the scenario. Anyway, "instantaneous" and newtonian physics do not mix well, and that is where the mathematical model of human body as an idealised moving point breaks down. And ultimately it is not the acceleration that is responsible for your demise when you hit the ground, but the (rather abrupt) displacement of your tissues :-).Consider the time reversed scenario, you are at constant 1g, say, standing on a high platform, and the situation suddenly changes into 0g - the platform instantaneously disintegrates and you start free fall. That's hardly fatal. – Radovan Garabík Oct 04 '15 at 19:09
  • Also, fighter pilots experience G forces in different directions than constant thrust - which is a huge problem for the human body. Position the body correctly, and things are a lot better. – user3082 Oct 04 '15 at 19:39
  • 3
    This does not meet the standards of the [tag:hard-science] tag. Citations, please. – HDE 226868 Oct 04 '15 at 20:42